지금까지는 3차원 공간에서 존재하는 물체의 자세와 위치에 대해서 표현하는 방법을 공부했다. 우리는 자세와 위치를 표현하기 위해서 transformation matrix 을 이용했고 이러한 행렬들의 모임을 \(SE(3)\) 라고 했다. 이번에는 3차원 공간에서의 움직임에 대해 공부해보자.
Twists
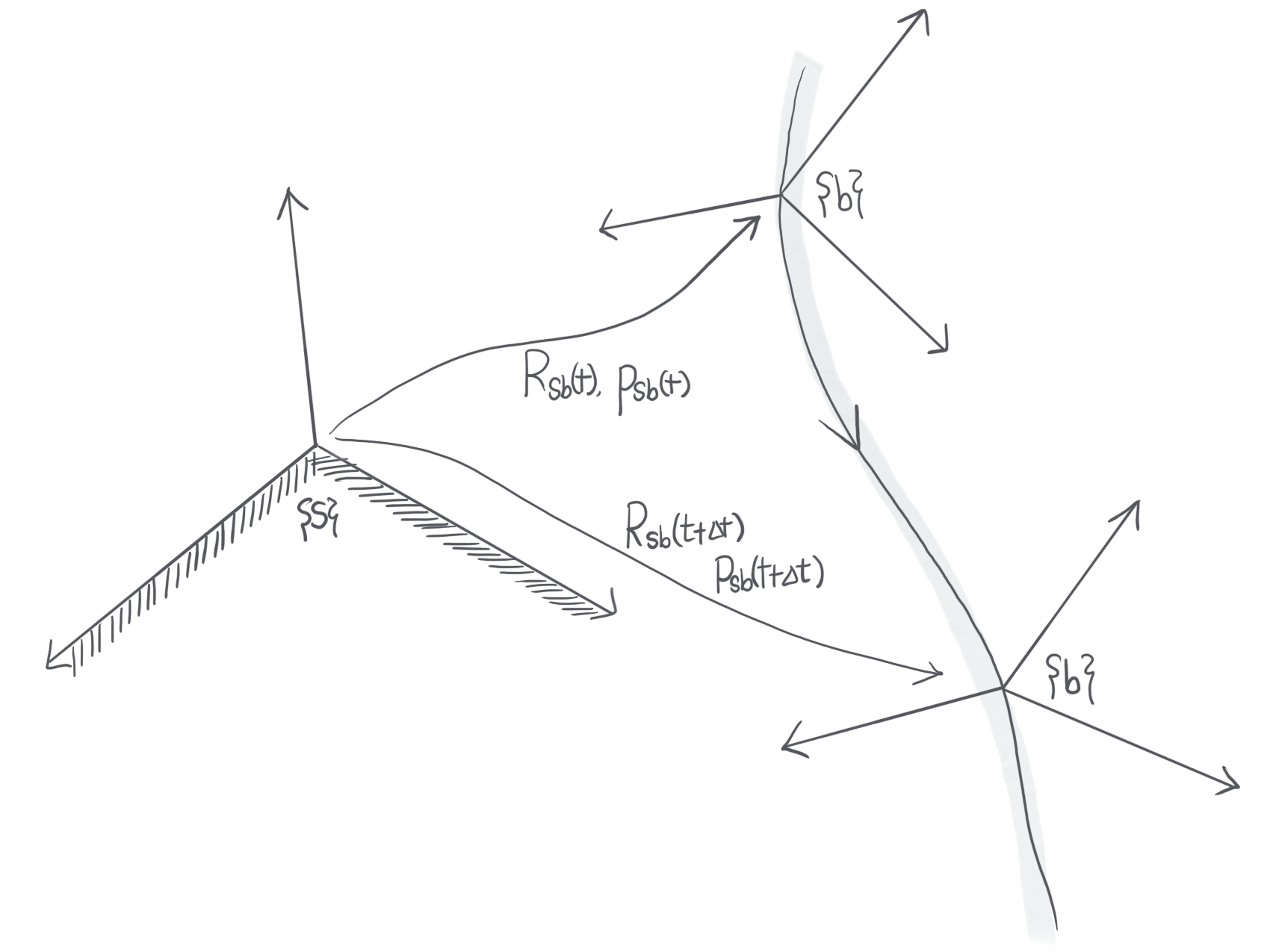
시간 \(t\) 에서 frame \(\{b\}\) 의 transformation matrix 를 frame \(\{s\}\) 을 기준으로 표현하면
\(T_{sb}(t)=T(t)=\left[\begin{array}{c|c}R(t) & p(t) \\ \hline 0 & 1 \end{array}\right]\)
라 하자. 우리는 시간 \(t\) 에서의 각속도를 다음과 같이 구했다.
\(\left[\omega_b\right] = R^{-1}\dot{R}\)
이와 비슷하게 한번 \(T^{-1}\dot{T}\) 를 계산해보자.
\(\begin{align} T^{-1}\dot{T} &= \left[\begin{array}{cc}R^\text{T} & – R^\text{T}p \\ 0 & 1 \end{array}\right]\left[\begin{array}{cc}\dot{R} & \dot{p} \\ 0 & 0 \end{array} \right] \\ &= \left[\begin{array}{cc} R^\text{T}\dot{R} & R^\text{T}\dot{p} \\ 0 & 0 \end{array}\right] \\ &= \left[\begin{array}{cc} \left[\omega_b\right] & v_b \\ 0 & 0 \end{array}\right]\end{align}\)
우리는 각속도에 대해서 이미 공부했으므로 \(\left[\omega_b\right] = R^\text{T}\dot{R}\) 은 frame \(\{b\}\) 에서 표현한 회전 각속도를 \(3\times3\) skew-symmetric matrix 로 표현했다는 것을 이미 알고 있다. 그러면 \(v_b\) 는 어떻게 설명 할 수 있을까?
우선 \(v_b\) 를 이루고 있는 \(\dot{p}\) 와 \(R^\text{T} = R_{bs}\) 에 대해서 생각해보자. \(p\)는 frame \(\{b\}\) 의 원점 위치를 frame \(\{s\}\) 를 기준으로 표현한 것이다. 그러면 \(\dot{p}\) 은 frame \(\{b\}\) 의 원점의 속도를 frame \(\{s\}\) 의 입장에서 서술한 것이라는걸 알 수 있을 것이다. \(R^\text{T}=R_{bs}\) 는 frame \(\{b\}\) 에서 바라본 frame \(\{s\}\) 의 자세이므로 \(R^\text{T}\dot{p}\) 는 \(\dot{p}\) 의 기준 frame 을 \(\{s\}\) 에서 \(\{b\}\) 로 옮긴것으로 생각 할 수 있다. 즉 \(v_b=R^\text{T}\dot{p}\) 는 frame \(\{b\}\)의 원점의 속도를 frame \(\{b\}\) 에서 표현한 것이다. 쉽게 설명하면 frame \(\{b\}\) 가 움직일때 frame \(\{b\}\) 위에 서있는 사람이 자기가 움직이는 속도를 본인 입장에서 서술했다고 생각하면 된다.
이제 각속도와 선속도를 한번에 서술하는 표현법에 대해서 살펴보자.
Definition
Given \(\omega_b, v_b \in \mathbb{R}^3\), the spatial velocity in the body frame, or simply the body twist, is defined as follows:
$$ \mathcal{V}_b=\left[\begin{array}{c} \omega_b \\ v_b \end{array}\right] \in \mathcal{R}^6.$$
Definition
Given spatial velocity \(\mathcal{V}_b \in \mathbb{R}^6\), define \(\left[\cdot\right]\) noation as
$$ T^{-1}T = \left[\mathcal{V}_b \right]=\left[\begin{array}{cc}\left[\omega_b\right] & v_b \\ 0 & 0 \end{array}\right] $$
The set of all \(4 \times 4\) matrices of the form is called \(se(3)\). \(se(3)\) is called the Lie algebra of the Lie group \(SE(3)\).
Spatial velocity 그리고 twist 개념이 여기서 등장한다. Body frame 에서 표현한 spatial velocity 는 \(\left[\begin{array}{c}\omega_b \\ v_b\end{array}\right]\) 로 각속도와 선속도를 동시에 담고 있다. 그리고 \(SE(3)\) 의 Lie algebra 인 \(se(3)\) (우리는 \(SE(3)\) 와 구별하기 위해 앞에 small 을 붙여서 말한다) 는 \(\left[\cdot\right]\) 기호를 이용해서 \(\left[\mathcal{V}_b\right]\) 로 쓴다.
고정 좌표계 frame \(\{s\}\) 기준으로 각속도를 \(\left[\omega_s\right]=\dot{R}R^\text{T}\) 처음 구했듯이 이번에는 \(\dot{T}T^{-1}\) 를 계산해보자.
\(\begin{align} \dot{T}T^{-1} &= \left[\begin{array}{cc} \dot{R} & \dot{p} \\ 0 & 0 \end{array}\right] \left[\begin{array}{cc} R^\text{T} & -R^\text{T}p \\ 0 & 1\end{array}\right] \\ &= \left[\begin{array}{cc} \dot{R}R^\text{T} & -\dot{R}R^\text{T}p+\dot{p} \\ 0 & 0 \end{array}\right] \\ &= \left[\begin{array}{cc} \left[\omega_s\right] & v_s \\ 0 & 0 \end{array}\right] \\ &= \left[\mathcal{V}_s\right] \in se(3) \end{align}\)
\(\omega_s\) 는 각속도 벡터를 frame \(\{s\}\) 기준으로 표현한 것이다. 그러면 \(v_s\) 는 뭘까? frame \(\{b\}\) 의 원점의 속도를 frame \(\{s\}\) 기준으로 표현한걸까?
정답은 ‘NO’다. 다시한번 \(v_s\) 를 살펴보자.
\(v_s = \dot{p}-\dot{R}R^\text{T}p = \dot{p} – \left[\omega_s\right]p\)
\(3\times3\) screw-symmetric matrix 는 외적을 나타내므로 \(\left(\left[\omega_s\right] = \omega_s \times\right)\)
$$v_s = \dot{p} + \omega_s \times (-p)$$
라는 결론을 얻을 수 있다. 이 식을 보면 \(\dot{p}, \omega_s, -p\) 모두 frame \(\{s\}\) 를 기준으로 표현한 값들이다. \(\dot{p}\) 는 frame \(\{b\}\) 의 원점의 속도, \(\omega_s\) 는 frame \(\{b\}\) 의 각속도 그리고 \(-p\) 는 frame \(\{b\}\) 의 원점에서부터 frame \(\{s\}\) 의 원점까지 벡터를 frame \(\{s\}\) 에서 표현한게 된다. 그러면 결론적으로 \(v_s\) 는 선속도 \(\dot{p}\) 에 frame \(\{b\}\)의 원점으로부터 \(-p\) 만큼 떨어진 곳 (frame \(\{s\}\)의 원점)의 회전에 의한 속도를 더한 값이 된다. 다시 말해서 \(v_s\)는 frame \(\{s\}\)의 원점의 속도를 frame \(\{s\}\) 에서 표현한게 된다. 음… 고정 좌표계의 원점의 속도라 이상하지 않은가. 설명을 보충하기 위해 아래 그림을 가지고왔다.
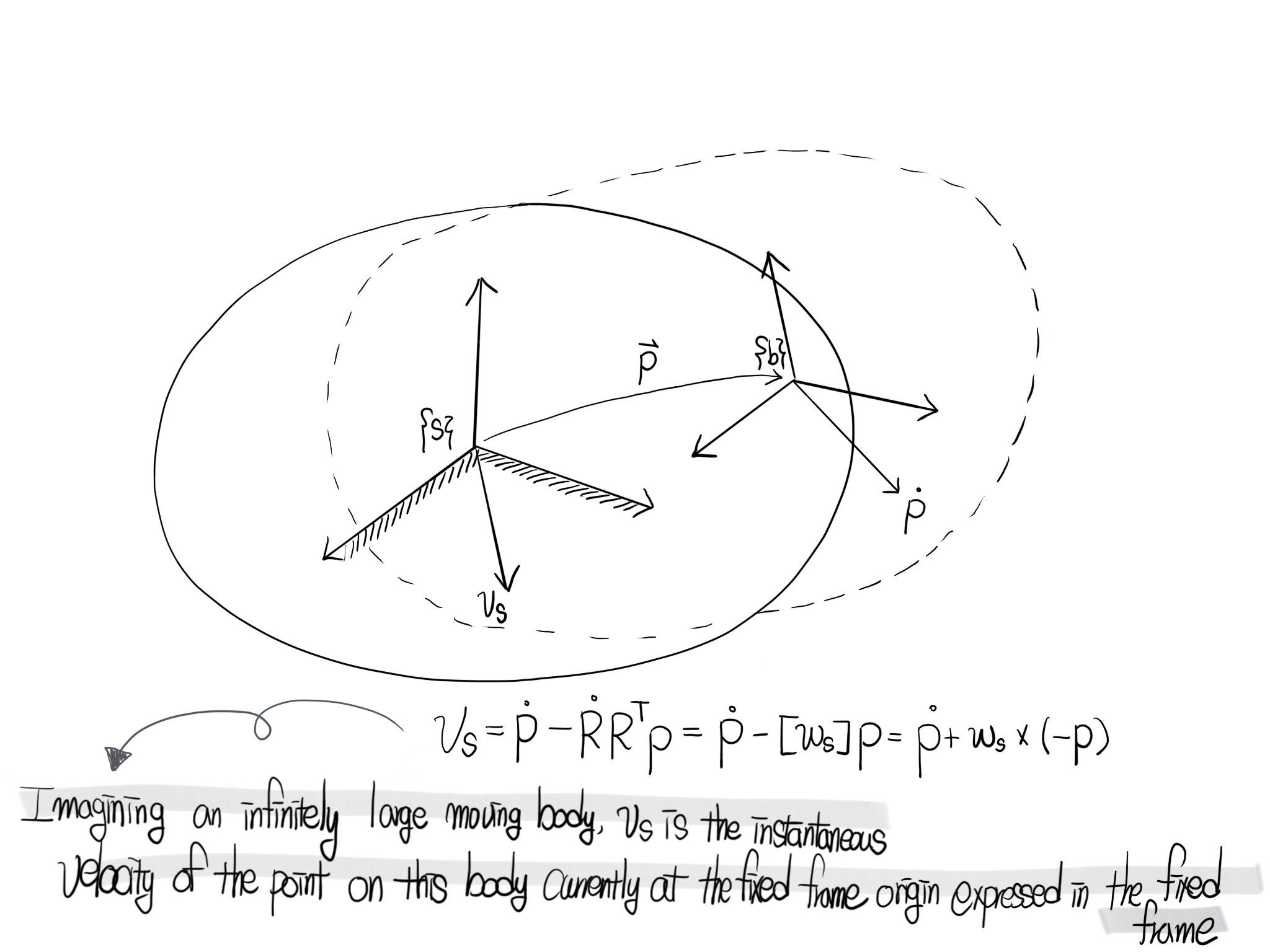
우리가 위에서 말한 고정 좌표계 frame \(\{s\}\) 의 원점이라는건 실제 frame \(\{s\}\) 을 말하는게 아니고 frame \(\{s\}\)의 원점과 같은 위치에 있는 가상의 점을 의미한다. 이 가상의 점은 움직 좌표계 frame \(\{b\}\)과 함께 움직인다. 그림 [3]을 보면 frame \(\{b\}\)와 함께 움직이는 큰 물체를 생각하고 그 물체에 frame \(\{s\}\) 의 원점과 같은 위치에 있는 점을 찍은 다음에 그 점이 움직이는 속도를 frame \(\{s\}\)에서 표현하는 것이다. 물론 움직일때마다 그 점의 위치는 계속 바뀐다. 헷갈릴 수 있는데 나중에도 또 다루는 내용이고 중요한 내용이므로 꼭 이해하고 넘어가길 바란다.
$$\mathcal{V}_s\text{ : Spatial velocity in the space frame, or simply the spatial twist}$$
이제 우리는 움직이는 frame 의 속도 (각속도와 선속도)를 frame \(\{s\}\) 에서 표현한 것과 frame \(\{s\}\) 에서 표현하는 방법에 대해서 배웠다.
\(\mathcal{V}_s\) 와 \(\mathcal{V}_b\) 의 관계
\(\left[\mathcal{V}_b\right] = T^{-1}\dot{T}\) 이므로 \(\dot{T} = T\left[\mathcal{V}_b\right]\) 인 사실을 생각하면서 \(\left[\mathcal{V}_s\right]\) 을 \(\left[\mathcal{V}_b\right]\) 에 대해 정리하면
\(\begin{align} \left[\mathcal{V}_s\right] &= \dot{T}T^{-1} \\ &= T\left[\mathcal{V}_b\right]T^{-1} \\ &= \left[\begin{array}{cc} R\left[\omega_b\right]R^\text{T} & -R\left[\omega_b\right]R^\text{T}p + Rv_b \\ 0 & 0 \end{array}\right] \end{align} \)
이 된다. 위 식을 다시 쓰면
$$\mathcal{V}_s = \left[\begin{array}{cc} R & 0 \\ [p]R & R \end{array}\right]\mathcal{V}_b$$
여기서 \(\mathcal{V}_s = \left[\begin{array}{c} \omega_s \\ v_s \end{array}\right]\), \(\mathcal{V}_b = \left[\begin{array}{c} \omega_b \\ v_b \end{array}\right]\), \(R=R_{sb}\) 그리고 \(p=p_{sb}\) 이다.
Definition
Given \(T=(R, p) \in SE(3)\), its adjoint representation \([\text{Ad}_\text{T}]\) is
$$[\text{Ad}_T] = \left[\begin{array}{cc} R & 0 \\ [p]R & 0 \end{array}\right] \in \mathbb{R}^{6\times6}.$$
Adjoint mapping 을 나타내는 방법은 두가지가 있다. \(\mathcal{V}^\prime = [\text{Ad}_T]\mathcal{V}\) 또는 \(\mathcal{V}^\prime = \text{Ad}_T(\mathcal{V})\) 처럼 쓰고 계산은 \( [\text{Ad}_T] = \left[\begin{array}{cc} R & 0 \\ [p]R & 0 \end{array}\right]\) 을 이용하거나 \(\left[\mathcal{V}^\prime\right] = T \left[\mathcal{V}\right]T^{-1}\) 을 이용한다.
Properties of Adjoint Map
- Let \(T_1, T_2 \in SE(3)\), and \(\mathcal{V} = (\omega, v)\). Then,
$$ \text{Ad}_{T_1}(\text{Ad}_{T_2}(\mathcal{V})) = \text{Ad}_{T_1 T_2}(\mathcal{V}), [\text{Ad}_{T_1}][\text{Ad}_{T_2}]\mathcal{V}=[\text{Ad}_{T_1 T_2}]\mathcal{V}.$$
- For any \(T \in SE(3)\) the following holds:
$$[\text{Ad}_T]^{-1} = [\text{Ad}_{T^{-1}}].$$
- 어떤 회전하는 frame \(\{b\}\) 에 대해서 twist 를 \(\mathcal{V}_s\) 와 \(\mathcal{V}_b\) 이라 했을 때 아래와 같은 식을 만족한다.
$$ \begin{align} \mathcal{V}_s &= [\text{Ad}_{T_{sb}}]\mathcal{V}_b \\ \mathcal{V}_b &= [\text{Ad}_{T_{sb}^{-1}}]\mathcal{V}_s \end{align} $$